Physics-Informed Models for Motor Design Optimization
This case study developed in collaboration with Pilabz electro mechanical systems and CEET, IIT Madras, presents an AI-driven approach to predict and control air gap flux in electro-mechanical systems, specifically Internal Permanent Magnet Synchronous Motors (IPMSM). By using neural networks, we efficiently calculate flux distributions and automatically adjust motor parameters, eliminating the need for trial-and-error methods. This innovation streamlines motor design and optimization with minimal latency.
This work was done as a short-term consultative engagement between SupportVectors AI Lab, Pilabz electro mechanical systems and CEET, IIT Madras.
Opportunity
The Challenge of Optimizing Motor Geometries
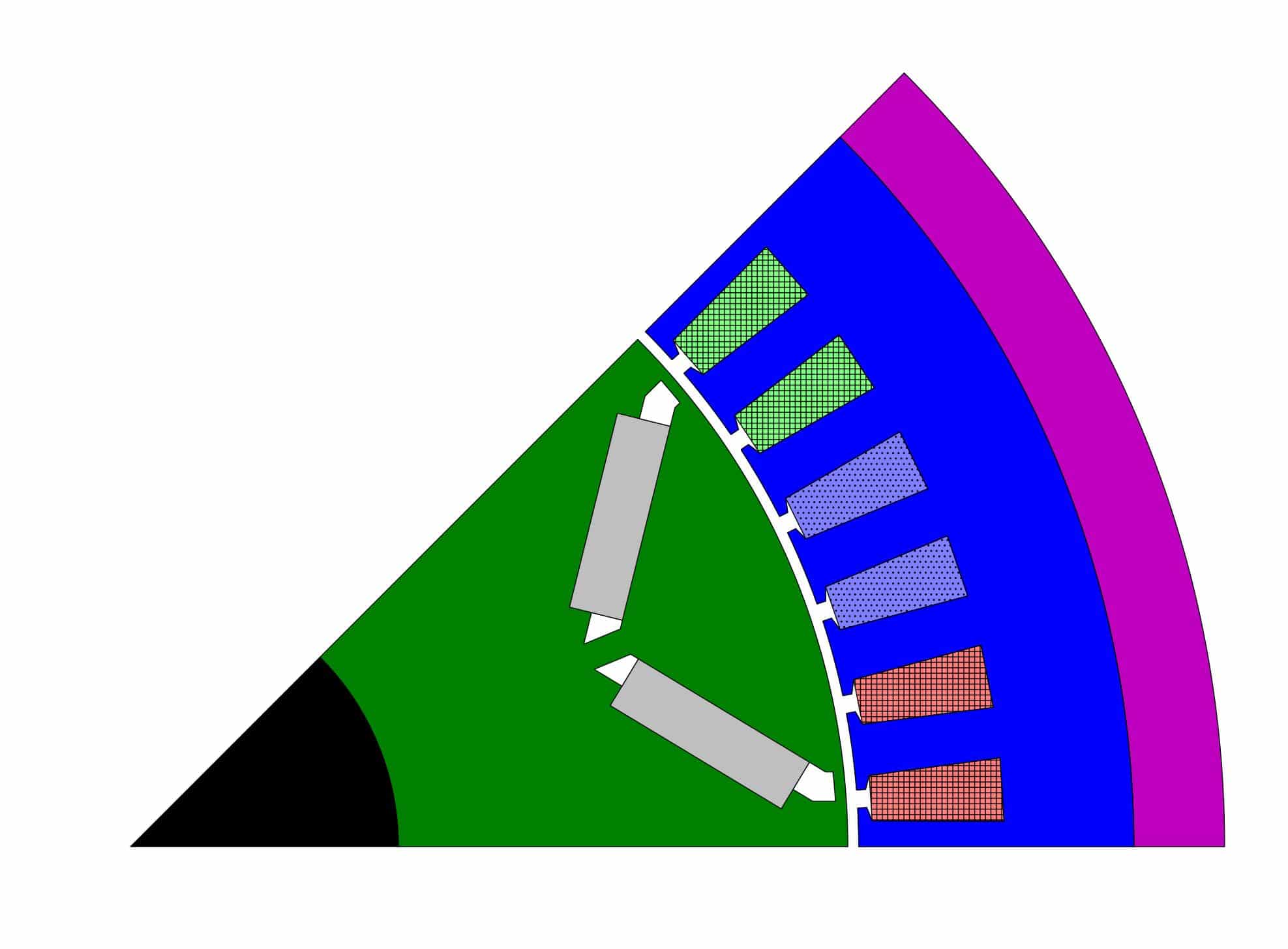
In electric motors, particularly in Internal Permanent Magnet Synchronous Motors (IPMSM), the magnetic flux plays a crucial role in determining motor efficiency and performance. The air gap magnetic flux refers to the magnetic field that exists between the stator (the stationary part) and rotor (the rotating part) of the motor. This flux is essential for driving the motor’s torque and ensuring smooth operation. However, calculating this flux accurately is complex, especially when dealing with different motor geometries or specific use cases.
IPMSMs are widely used in various applications, from electric vehicles to industrial machinery, due to their efficiency and high performance. However, the current methods used to calculate the air gap flux are cumbersome and slow. These methods require detailed simulations and iterative adjustments to find the optimal motor geometry, a process that can be time-consuming and impractical for real-time applications. The lack of a faster, automated method to calculate and optimize the flux distribution limits the ability to make quick design adjustments, hindering innovation and slowing down the motor design process
The objective of this project was to develop an AI-driven solution to efficiently calculate the air gap magnetic flux in Internal Permanent Magnet Synchronous Motors (IPMSM) with minimal latency, and to replace the traditional trial-and-error approach by automatically adjusting motor geometry parameters for optimal flux distribution.
Solution
Automating Motor Optimization with AI-Driven Models
To address the challenge of efficiently calculating the air gap magnetic flux and optimizing motor geometry, we experimented with several different neural network architectures. The solution revolved around training a neural network to learn the relationship between motor geometry parameters and the resulting flux distribution, thus eliminating the need for complex simulations and reducing computation time.
Review of Related Work
- CNNs for Steady Flow Approximation: Ideas from this research highlighted how convolutional neural networks could model physical phenomena efficiently, influencing the choice of network architectures. [2]
- Physics-Informed Neural Networks (PINNs): The use of PINNs in other applications demonstrated how physics-based constraints could enhance model accuracy by incorporating governing equations directly into the loss function. [3][4]
- Dynamic System Simulation: Techniques from prior work in dynamic systems helped refine the strategy for auto-adjusting geometry parameters using neural networks.[5]
1. Data Collection and Preprocessing
We began by gathering a dataset that included various motor geometries and their corresponding magnetic flux distributions. This data was derived from Finite Element Method Magnetics (FEMM) [1] simulations, which is a common approach for calculating flux distributions. The input parameters for the model included motor geometry features like rotor and stator dimensions, material properties, and other design specifications. These features, along with the corresponding magnetic flux distribution for each geometry, formed the basis of our training data.

Input parameters for the model
2. Neural Network Architecture Design
Given the varying nature of motor geometries, we designed distinct neural network architectures for different types of geometry. We experimented with two major types of geometries:
Flat-type Geometry Neural Architecture: This architecture was designed to model geometries where the rotor and stator were aligned in a flat configuration.
V-type Geometry Neural Architecture: For geometries with a more angled rotor and stator, this architecture was used.
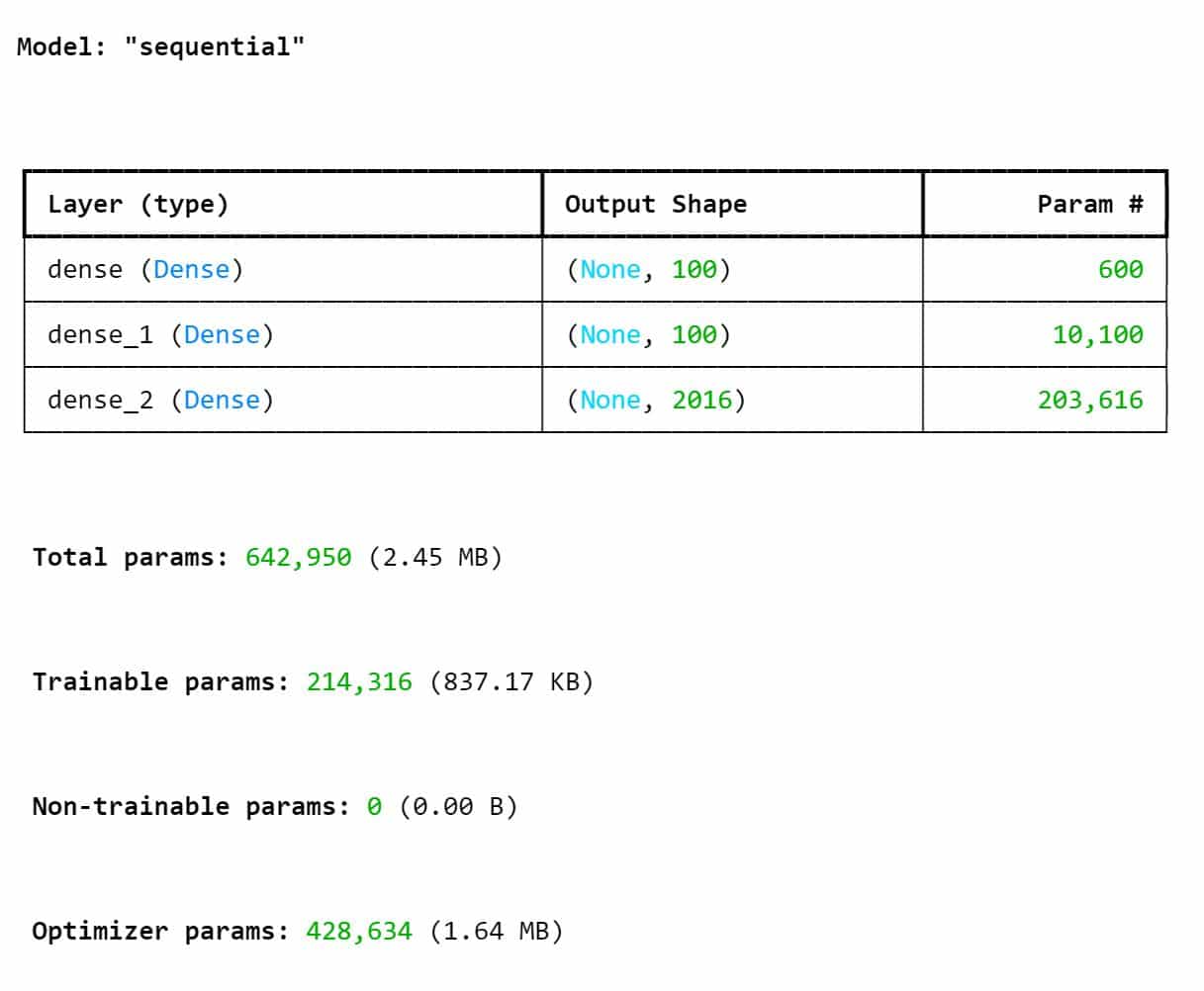
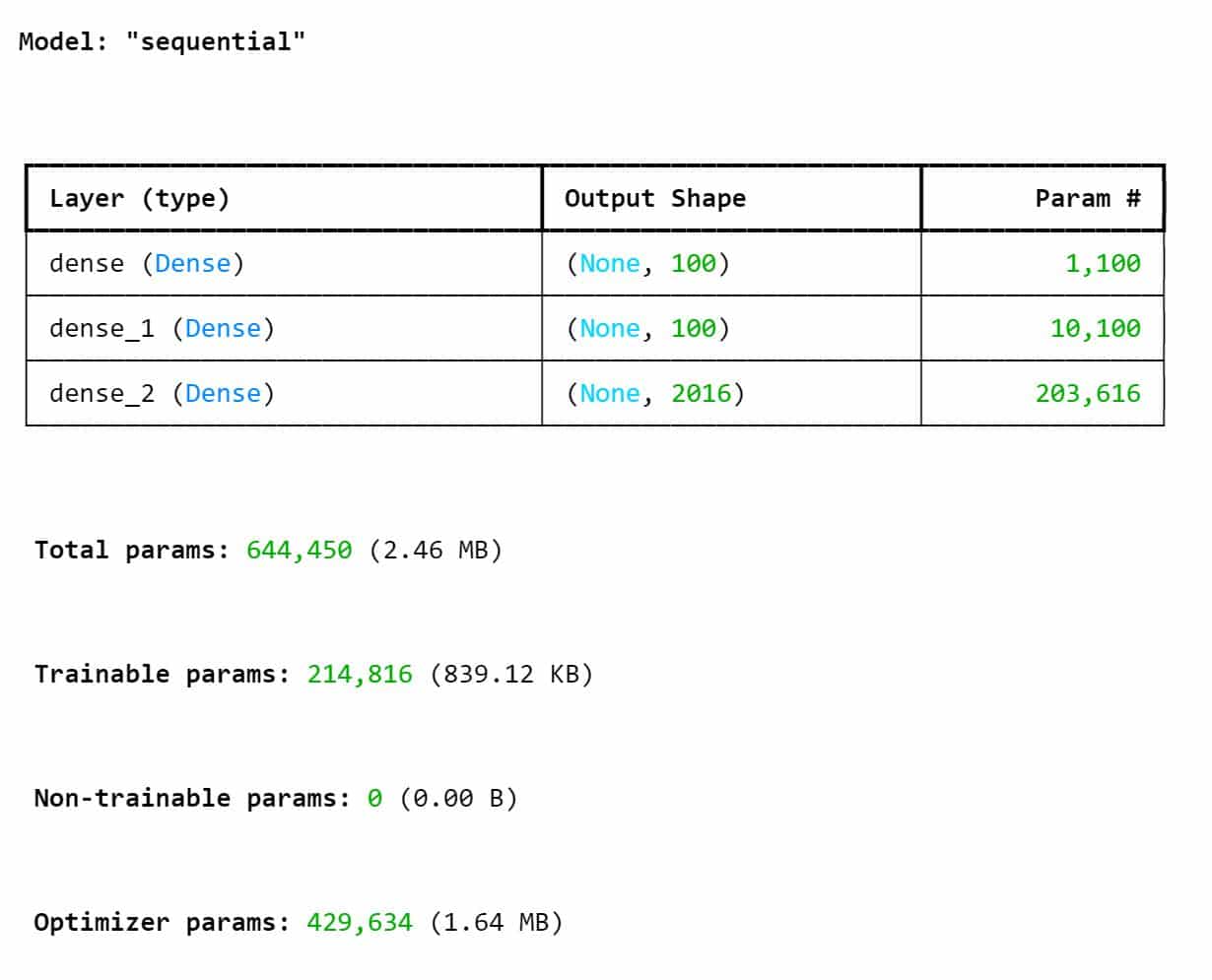
Each network was tailored to capture the specific relationships between the input parameters and the magnetic flux distribution of that geometry type. The architecture for both networks consisted of a series of fully connected layers, with the final layer producing the flux distribution across the air gap.
3. Control Flow for Auto-adjusting Geometry Parameters
To go beyond just predicting flux, we developed a second neural network, NN1, that could automatically adjust the geometry parameters to achieve a desired flux distribution. The input to NN1 was a set of key flux features, such as peak flux values, the angle of peak flux, periodicity, and points where the flux reached specific fractions of the peak value. The output of NN1 was a set of geometry parameters that, when fed into NN2 (the trained neural network), would result in the desired flux distribution.
We synthetically generated training data for NN1 by sampling a wide range of flux distributions and extracting key features. This allowed NN1 to learn the mapping from desired flux features to the corresponding motor geometry parameters.
Once trained, NN1 could take a set of desired flux features as input and output the necessary geometry parameters. These parameters could then be passed to NN2, which would compute the final flux distribution based on the optimized geometry. This approach not only automated the flux prediction but also provided a mechanism for optimizing motor geometry in real-time to achieve specific performance outcomes.

Impact

V-Type Geometry Model Performance

Flat-Type Geometry Model Performance
Faster, Smarter Motor Design
The enhanced deep learning models significantly outperformed expectations in predicting airgap magnetic flux for different motor geometries. For flat-type motors, the test loss (Mean Squared Error) was reduced to 0.055 with a Test Mean Absolute Error (MAE) of 0.127, achieving an R² score of 0.91. Similarly, for V-type motors, the test loss was as low as 0.009 with a Test MAE of 0.044, and an impressive R² score of 0.99.
These results demonstrate a remarkable improvement in prediction accuracy, showcasing the model’s ability to generalize across different motor types. The streamlined solution accelerates the motor design process, enhances predictive capabilities, and reduces the reliance on extensive FEA simulations.